- Difficoltà: facile
- Lezioni previste: 1
- Tempo medio di apprendimento: 7 giorni
- Percentuale risposte per avanzamento: 80%
• Per intervallo si intende la distanza fra due suoni siano essi in successione melodica o simultanei.
• L'intervallo si definisce con due parametri: distanza e qualità
La distanza non è altro che il conteggio delle note fra il primo e il secondo suono dell'intervallo e si indica con i numeri ordinali:
 |
La difficoltà nasce invece quando si deve calcolare la qualità dell'intervallo in quanto, stabilito che si tratta di una terza, occorre specificare che tipo di terza perché ne esistono di diverse varietà! (do#-Mi /do-mib/ do#-mi# ecc).
Tradizionalmente si insegna a calcolare tale qualità facendo riferimento alla tonalità.
Tale metodo, a parte essere macchinoso
e non applicabile ad intervalli che inziano da una nota non tonica di una tonalità (Es mi#), è lento e non utilizzabile per la musica
atonale o liberamente tonale.
Propongo quindi un semplice sistema che parte dagli intervalli diatonici (senza alterazioni) per poi derivarne la qualità mediante l'aggiunta delle alterazioni che ne modificano l'ampiezza attraverso il misuratore standard seguente:
La corretta terminologia per misurare la qualità degli intervalli e che permette di avere un valore per qualsiasi intervallo è la seguente:
| Dal + grande | ||
|---|---|---|
| +E | + che eccedente | |
| E | eccedente | |
| +A | + che aumentato | |
| A | aumentato | |
| G Giusti per Unis, 4° e 5° | M | maggiore |
| m | minore | |
| D | diminuito | |
| +D | + che diminuito | |
| DF | deficente | |
| +DF | + che deficente | |
| Al + piccolo | ||
Il metodo consiste in due step
Definire la qualità dell'intervallo diatonico senza considerare le eventuali alterazioni
 |
Prendendo come esempio: sol bemolle si# inziamo considerando prima l'intervallo diatonico senza alterazioni Sol-Si e poi successivamente, come sarà spiegato nello step 2, aggiungeremo le alterazioni
A questo punto occorre conoscere alla perfezione tutti gli intervalli diatonici.
Anche se consiglio di imparali a memoria, fornisco una
tavola per facilitare la loro memorizzazione
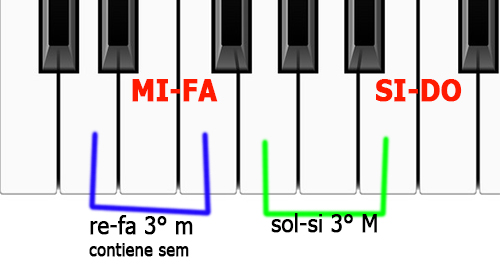
Gli intervalli diatonici sono tutti maggiori tranne quelli che contengono 1 o 2 fra i semitoni MI-FA o SI-DO
In particolare:
• La presenza di uno dei due semitoni "minorizza" sino alla terza
• La presenza di entrambi semitoni "minorizza" gli intervalli superiori alla terza
(ovviamente "rende diminuiti" 4° e 5° che non hanno Maggiore/minore)
 |
Tabella per tutti gli intervalli diatonici
| Intervallo | Qualità |
|---|---|
| Unis | Giusto |
| 2° | diventa minore se contiene uno fra i sem Mi-Fa o Si-Do altrimenti è Maggiore |
| 3° | diventa minore se contiene uno fra i sem Mi-Fa o Si-Do altrimenti è Maggiore |
| 4° | diventa aumentata se contiene entrambi i semitoni Mi-Fa o Si-Do altrimenti è Giusta (l'unica aumentata è Fa-Si) |
| 5° | diventa diminuita se contiene entrambi i semitoni Mi-Fa o Si-Do altrimenti è Giusta (l'unica diminuita è Si-Fa) |
| 6° | diventa minore se contiene entrambi i semitoni Mi-Fa o Si-Do altrimenti è Maggiore |
| 7° | diventa minore se contiene entrambi i semitoni Mi-Fa o Si-Do altrimenti è Maggiore |
| 8° | Giusto |
 |
Per comodità: negli gli intervalli melodici discendendi calcolare l'intervallo sempre partendo dalla nota più bassa ossia leggendolo in maniera ascendente
Riepilogo di tutti gli intervalli diatonici
Con evidenziati i semitoni che ne cambiano il modo
 |
| Intervalli naturali |
| |||||||||||
|
0/30 |
|
Solo dopo aver acquisito familiarità con gli intervalli diatonici si proceda con lo STEP 2
Una volta stabilità la qualità dell'intervallo diatonico, aggiungere le alterazioni una alla volta modificando la qualità in base alla tabella a seconda che l'alterazione che si aggiunge ingrandisca o rimpicciolosca l'intervallo
Esempio di procedimento passo passo per calcolare l'intervallo Sol bemolle-Si#
| passo 1 | tolgo le alterazioni e lo calcolo come diatonico | Sol-Si | 3° M |
|---|---|---|---|
| passo 2 | Aggiungo il bemolle a sol e vedo che l'intervallo si è ingrandito. Consultando lo schema vedo che la misura di un grado oltre il maggiore è Aumentato | Solbem-Si | 3° A |
| passo 3 | Aggiungo il diesis al SI e vedo che l'intervallo si ingrandisce ancora quindi consultando lo schema salgo ancora di un grado e trovo: + che Aumentato | Solbem-Si# | 3° +A |
Esempio di procedimento passo passo per calcolare l'intervallo DO# Fa bemolle
| passo 1 | tolgo le alterazioni e lo calcolo come diatonico | Do-Fa | 4° G |
|---|---|---|---|
| passo 2 | Aggiungo il # a DO e vedo che l'intervallo si restringe. Consultando lo schema vedo che la misura di un grado più piccola del giusto è: Diminuito | Do#-Fa | 4° D |
| passo 3 | Aggiungo il bemolle al FA e vedo che l'intervallo si restringe ancora quindi consultando lo schema scendo ancora di un grado e trovo: + che Diminuito | Do#-Fabem | 4° +D |
Si noti come il procedimento è estremamente semplice per intervalli che, col sistema tradizionale delle scale, sarebbe stato particolarmente arduo da identificare.
Si provi con intervalli del tipo: fa bem- Si# o Do doppio# Fa bemolle, assolutamente impossibili da calcolare col sistema tonale.
Per le altreazioni uguali nei due suoni si può operare il meccanismo della "semplificazione" in quanto: se un # al suono basso restringe l'intervallo, un # al suono alto lo riallarga riportandolo allo stato originario.
 |
| Intervalli cromatici |
| |||||||||||
|
0/40 |
|
| + grande | |
|---|---|
| +E | |
| E | |
| +A | |
| A | |
| G per Unis, 4° e 5° | M |
| m | |
| D | |
| +D | |
| DF | |
| +DF | |
| + piccolo | |

+ |
- |